Confruntarea Nicușor Dan - Cristian Tudor Popescu pe o problemă de matematică
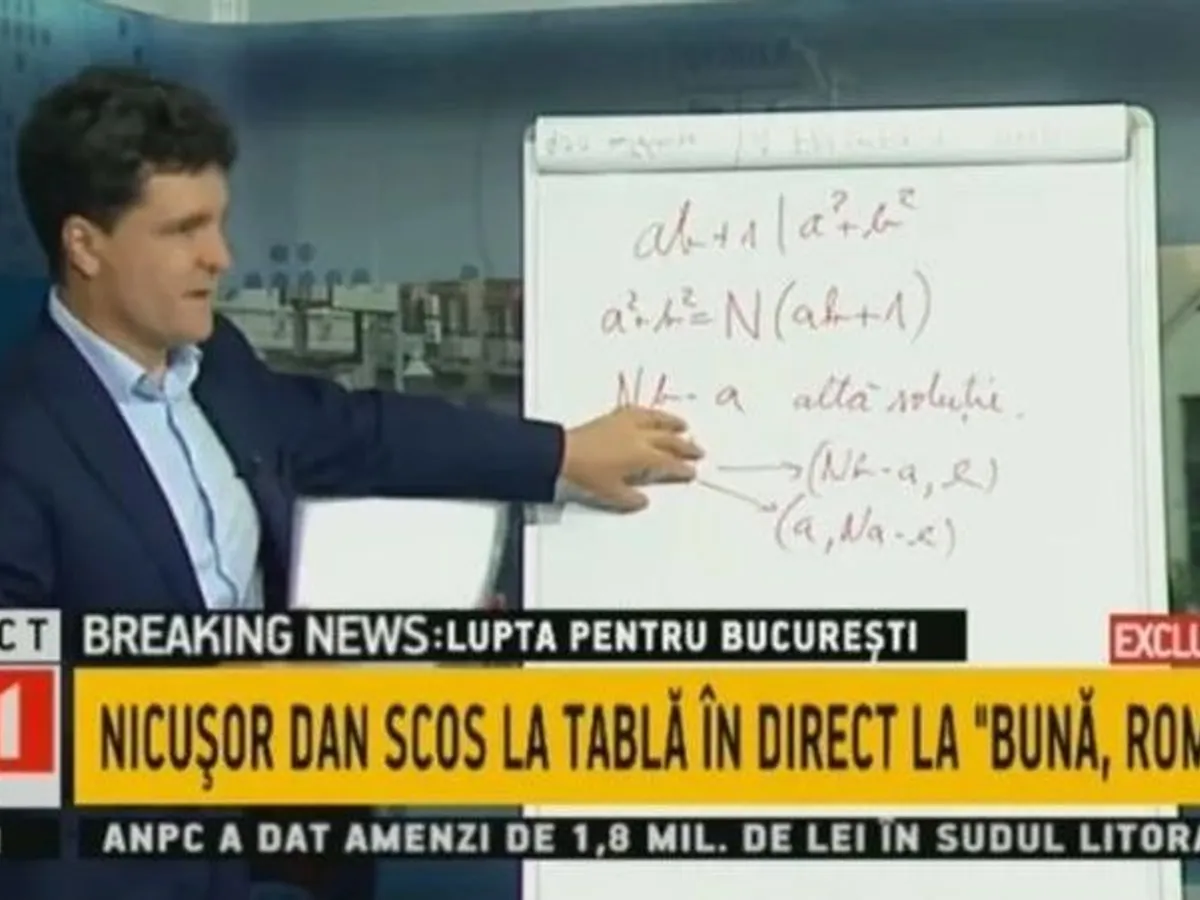
Nicușor Dan a explicat la B1 TV, în urma solicitării unui jurnalist, soluția pe care a dat-o „Problema nr. 6” la Olimpiada Internațională de Matematică de la Canberra, din 1988.
Nicușor Dan, actualmente candidat pentru Primăria Generală a Capitalei, a câștigat aurul olimpic, în urmă cu 32 de ani, după ce a rezolvat această problemă.
„Linia generală a raționamentului este corectă și frumoasă, dar am câteva observații”, a scris, ulterior, Cristian Tudor Popescu, cu privire la modul cum a rezolvat politicianul, la televizor, respectiva problemă de olimpiadă internațională. Totodată, jurnalistul a prezentat și 5 observații ale sale cu privire la soluția dată de Nicușor Dan.
„1. La punctul iii)., reprodus mai sus, în ipoteza b^2 – N > 0, folosind formula Vieta a produsului rădăcinilor, rezultă a(Nb-a)= b^2-N. De aici, afirmă dl Dan, ar rezulta că termenul (Nb-a) este negativ. Ceea ce este imposibil: a este pozitiv, b^2-N este pozitiv, deci produsul a două numere este pozitiv, unul dintre ele este pozitiv, deci și celălalt nu poate fi decât pozitiv, nicidecum negativ”, a scris Cristian Tudor Popescu.
Restul observațiilor pot fi citite aici.
Reacția lui CTP a devenit virală pe Facebook, utilizatorii acestei rețele de socializare fiind fascinați că în 2020, într-o țară cu educație în degringoladă și cu politicieni cu diplome mincinoase, poate avea loc o dezbatere publică pe o problemă de matematică.
Nicușor Dan i-a și răspuns jurnalistului, tot pe Facebook.
„„În primul rând vă mulţumesc pentru atenţie şi pentru observaţii. Intuiţia de la punctul iii este corectă, adică expresia (a^2+b^2)/(ab+1) “are ordinul de mărime a lui a/b deci este mai mare decât N”. Însă trebuie să avem mai multă atenţie la estimări pentru a ajunge la rezultat.
Deci punctul iii trebuie înlocuit cu următoarele:
iii. Dacă b^2 – N < 0, folosim a doua relaţie între rădăcinile ecuaţiei de gradul 2, a(Nb-a) = b^2 – N. Rezultă că Nb-a este negativ, deci că a > Nb. [aici intervine a treia observaţie/intuiţie, cu cât raportul a/b este mai mare, cu atât numărul (a^2+b^2)/(ab+1) este mai mare, şi pare că va fi prea mare].
Întrucât a, b şi N sunt numere naturale rezultă că a este cel puţin egală cu Nb+1. Notam x raportul dintre a-1 şi b, adică a = bx +1. x este mai mare sau egal cu N.
Înlocuim acum a în funcţie de b şi x în expresia (a^2+b^2)/(ab+1). Obţinem fracţia
(x^2 b^2 + 2xb + b^2 +1)/(xb^2 +b + 1) care e evident mai mare decât x deci mai mare decât N. Asta încheie punctul iii.
Toate întrebările dumneavoastră se referă la punctul iii pe care l-am modificat cu totul, dar le răspund şi punctual, pentru completitudine:
1. Contradicţia vine din eroarea mea de tastare. Cazul ii a fost b^2 – N > 0, cazul iii este b^2 – N < 0 şi nu > 0 cum am tastat.
2. Aveţi dreptate, am omis un +1, formula corectă este (a^2+b^2)/(ab+1)= (a/b+b/a) (1-1/(ab+1)). Asta nu e esenţial în estimare.
3. Aici nu e nicio greşeală. Funcţia x + 1/x este crescătoare pentru x mai mare sau egal cu 1 (căci de exemplu derivată sa este 1-1/x^2, dar se poate şi cu un calcul direct simplu) şi din ipoteza a/b este mai mare sau egal cu 1.
4. Aici este într-adevăr eroarea de estimare. Grăbindu-mă am încurcat între ele ipotezele.
5. Dacă 4 ar fi adevărat am avea ca (a^2+b^2)/(ab+1) ar fi cel puţin (N+1/N)(1-1/N^3)=N(1+1/N^2)(1-1/N^3)=N(1+1/N^2-1/N^3-1/N^5). Trebuie să demonstrăm că 1/N^2-1/N^3-1/N^5 este pozitiv deci că N^3 – N^2 – 1 este pozitiv. Această relaţie este adevărată pentru orice număr natural N mai mare ca 1 (1 este pătrat perfect deci putem exclude cazul N=1): de exemplu N^3 este cel puţin 2N^2 = N^2 + N^2 care este cel puţin N^2 + 4 din ipoteza N natural mai mare decât 1.
În concluzie politicienii - matematicieni nu mai trebuie provocaţi pe probleme de matematică în campanie căci se grăbesc şi pot greşi. Am glumit. Mi-a făcut plăcere şi să rezolv după 32 de ani problema de la olimpiada şi să răspund observaţiilor dumneavoastră.”